Skip to main content

Understanding Conditional Variational Autoencoders

Add caption

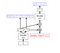
The variational autoencoder or VAE is a directed graphical generative model which has obtained excellent results and is among the state of the art approaches to generative modeling. It assumes that the data is generated by some random process, involving an unobserved continuous random variable z. it is assumed that the z is generated from some prior distribution P_θ(z) and the data is generated from some condition distribution P_θ(X|Z), where X represents that data. The z is sometimes called the hidden representation of data X.

Like any other autoencoder architecture, it has an encoder and a decoder. The encoder part tries to learn q_φ(z|x), which is equivalent to learning hidden representation of data X or encoding the X into the hidden representation (probabilistic encoder). The decoder part tries to learn P_θ(X|z) which decoding the hidden representation to input space. The graphical model can be expressed as the following figure.

(source)

The model is trained to minimize the objective function

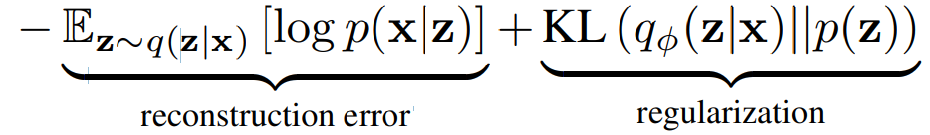
The first term in this loss is the reconstruction error or expected negative log-likelihood of the datapoint. The expectation is taken with respect to the encoder’s distribution over the representations by taking a few samples. This term encourages the decoder to learn to reconstruct the data when using samples from the latent distribution. A large error indicates the decoder is unable to reconstruct the data.

The second term is the Kullback-Leibler divergence between the encoder’s distribution q_φ(z|x) and p(z). This divergence measures how much information is lost when using q to represent a prior over z and encourages its values to be Gaussian.

During generation, samples from N(0,1) is simply fed into the decoder. The training and the generation process can be expressed as the following

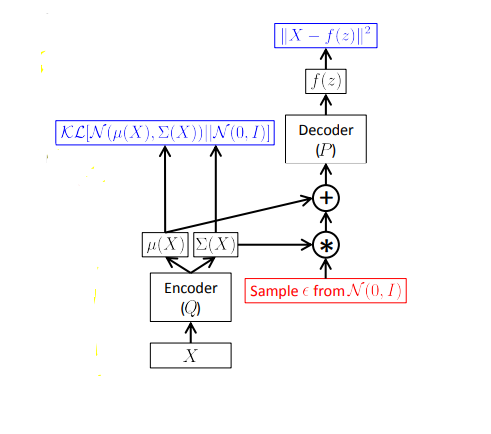
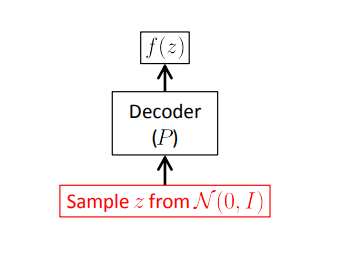
A training-time variational autoencoder implemented as a feedforward neural network, where P(X|z) is Gaussian. Red shows sampling operations that are non-differentiable. Blue shows the loss calculation. (source)
The testing-time variational “autoencoder,” which allows us to generate new samples. The “encoder” pathway is simply discarded. (source)

The reason for such a brief description of VAE is, it is not the main focus but very much related to the main topic.

The one problem for generating data with VAE is we do not have any control over what kind of data it generates. For example, if we train a VAE with the MNIST data set and try to generate images by feeding Z ~ N(0,1) into the decoder, it will also produce different random digits. If we train it well, the images will be good but we will have no control over what digit it will produce. For example, you can not tell the VAE to produce an image of digit ‘2’.

For this, we need to have a little change to our VAE architecture. Let’s say, given an input Y(label of the image) we want our generative model to produce output X(image). So, the process of VAE will be modified as the following: given observation y, z is drawn from the prior distribution P_θ(z|y), and the output x is generated from the distribution P_θ(x|y, z). Please note that, for simple VAE, the prior is P_θ(z) and the output is generated by P_θ(x|z).

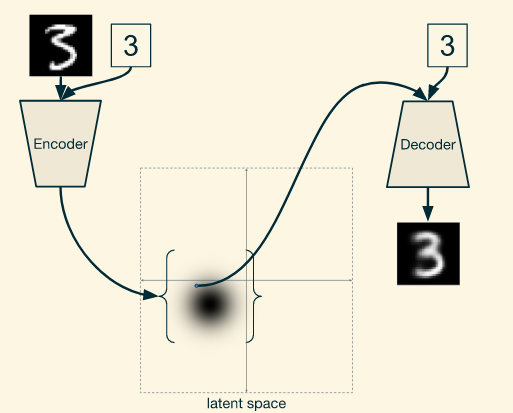
Visual representation task in conditional VAE (source)

So, here the encoder part tries to learn q_φ(z|x,y), which is equivalent to learning hidden representation of data X or encoding the X into the hidden representation conditioned y. The decoder part tries to learn P_θ(X|z,y) which decoding the hidden representation to input space conditioned by y. The graphical model can be expressed as the following figure.

(Source)

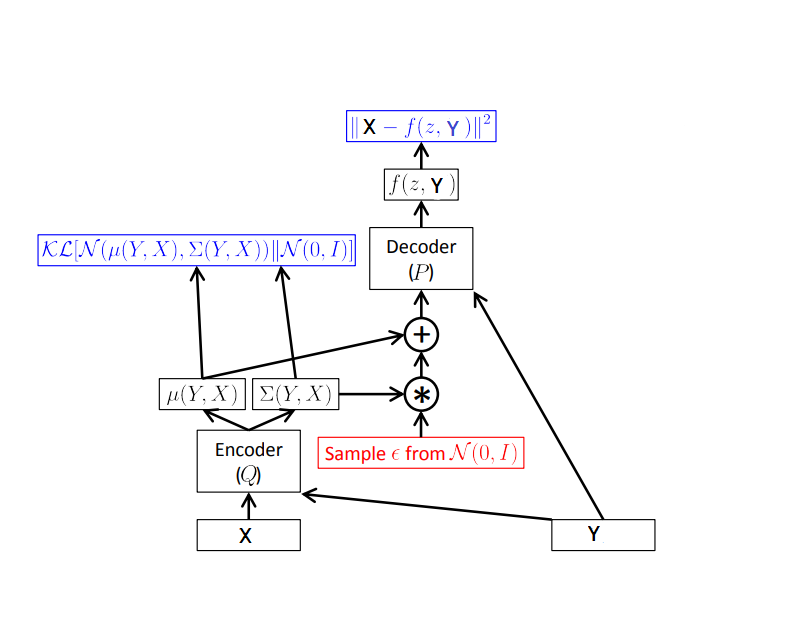
The neural network architecture of Conditional VAE (CVAE) can be represented as the following figure.

X is the image. Y is the label of the image which can be in 1 hot-vector representation. (modified from*)

The implementation of CVAE in Keras is available here.

References:

  1. Learning Structured Output Representation using Deep Conditional Generative Models
  2. Tutorial on Variational Autoencoders
  3. Auto-Encoding Variational Bayes

Popular posts from this blog

Neural Architecture Search (NAS)- The Future of Deep Learning

Most of us have probably heard about the success of ResNet, winner of ILSVRC 2015 in image classification, detection, and localization and Winner of MS COCO 2015 detection, and segmentation .  It is an enormous architecture with skip connections all over. While using this ResNet as a pre-trained network for my machine learning project, I thought “ How can someone come out with such an architecture? ’’ Large Human Engineered Architecture Soon after I learned that many engineers and scientists with their years of experience build this architecture. And there is more of a hunch than complete math that will tell you “ we need to have a 5x5 filter now to achieve the best accuracy ’’. We have wonderful architectures for the image classification task, but for other tasks, we have to spend much of our energy to find an architecture with reasonable performance for those tasks. It would certainly be better if we can automate this architecture modeling task just as we learn the parameters of ...
Read more

A Comprehensive Guide to the Correlational Neural Network with Keras

Human beings along with many other animals have 5 basic senses: Sight, Hearing, Taste, Smell, and Touch . We also have additional senses like a sense of balance and acceleration , a sense of time , etc. Every single moment the human brain processes information from all these sources and each of these senses affects our decision-making process. During any conversation, movement of lips, facial expression along with sound produced by vocal cord helps us to fully understand the meaning of words pronounced by the speaker. We can even understand words only by seeing the lips movement without any sound. This visual information is not just supplementary but necessary. This was first exemplified in the McGurk effect (McGurk & MacDonald, 1976) where a visual /ga/ with a voiced /ba/ is perceived as /da/ by most subjects. As we want our machine learning models to achieve human-level performance, it is also necessary to enable them to use data from various sources. In machine learning thes...
Read more